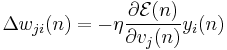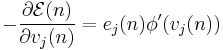Multilayer perceptron
A multilayer perceptron (MLP) is a feedforward artificial neural network model that maps sets of input data onto a set of appropriate output. An MLP consists of multiple layers of nodes in a directed graph, with each layer fully connected to the next one. Except for the input nodes, each node is a neuron (or processing element) with a nonlinear activation function. MLP utilizes a supervised learning technique called backpropagation for training the network.[1][2] MLP is a modification of the standard linear perceptron, which can distinguish data that is not linearly separable.[3]
Contents |
Theory
Activation function
If a multilayer perceptron has a linear activation function in all neurons, that is, a simple on-off mechanism to determine whether or not a neuron fires, then it is easily proved with linear algebra that any number of layers can be reduced to the standard two-layer input-output model (see perceptron). What makes a multilayer perceptron different is that each neuron uses a nonlinear activation function which was developed to model the frequency of action potentials, or firing, of biological neurons in the brain. This function is modeled in several ways, but must always be normalizable and differentiable.
The two main activation functions used in current applications are both sigmoids, and are described by
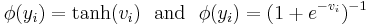 ,
,
in which the former function is a hyperbolic tangent which ranges from -1 to 1, and the latter, the logistic function, is similar in shape but ranges from 0 to 1. Here 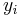 is the output of the
is the output of the  th node (neuron) and
th node (neuron) and 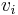 is the weighted sum of the input synapses. More specialized activation functions include radial basis functions which are used in another class of supervised neural network models.
is the weighted sum of the input synapses. More specialized activation functions include radial basis functions which are used in another class of supervised neural network models.
Layers
The multilayer perceptron consists of three or more layers (an input and an output layer with one or more hidden layers) of nonlinearly-activating nodes. Each node in one layer connects with a certain weight 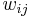 to every node in the following layer.
to every node in the following layer.
Learning through backpropagation
Learning occurs in the perceptron by changing connection weights after each piece of data is processed, based on the amount of error in the output compared to the expected result. This is an example of supervised learning, and is carried out through backpropagation, a generalization of the least mean squares algorithm in the linear perceptron.
We represent the error in output node  in the
in the  th data point by
th data point by 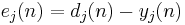 , where
, where  is the target value and
is the target value and  is the value produced by the perceptron. We then make corrections to the weights of the nodes based on those corrections which minimize the error in the entire output, given by
is the value produced by the perceptron. We then make corrections to the weights of the nodes based on those corrections which minimize the error in the entire output, given by
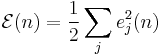 .
.
Using gradient descent, we find our change in each weight to be
where 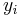 is the output of the previous neuron and
is the output of the previous neuron and 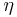 is the learning rate, which is carefully selected to ensure that the weights converge to a response fast enough, without producing oscillations. In programming applications, this parameter typically ranges from 0.2 to 0.8.
is the learning rate, which is carefully selected to ensure that the weights converge to a response fast enough, without producing oscillations. In programming applications, this parameter typically ranges from 0.2 to 0.8.
The derivative to be calculated depends on the induced local field 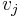 , which itself varies. It is easy to prove that for an output node this derivative can be simplified to
, which itself varies. It is easy to prove that for an output node this derivative can be simplified to
where 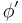 is the derivative of the activation function described above, which itself does not vary. The analysis is more difficult for the change in weights to a hidden node, but it can be shown that the relevant derivative is
is the derivative of the activation function described above, which itself does not vary. The analysis is more difficult for the change in weights to a hidden node, but it can be shown that the relevant derivative is
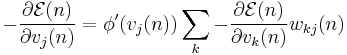 .
.
This depends on the change in weights of the  th nodes, which represent the output layer. So to change the hidden layer weights, we must first change the output layer weights according to the derivative of the activation function, and so this algorithm represents a backpropagation of the activation function. [4]
th nodes, which represent the output layer. So to change the hidden layer weights, we must first change the output layer weights according to the derivative of the activation function, and so this algorithm represents a backpropagation of the activation function. [4]
Border pairs method
is novel method for the learning of the MLP.[5] Connection weights are computed at once without iteration. Also near minimal configuration of the MLP is found. Only representative learning patterns are used for the learning. BPM do never stray in the local minima.
Applications
Multilayer perceptrons using a backpropagation algorithm are the standard algorithm for any supervised-learning pattern recognition process and the subject of ongoing research in computational neuroscience and parallel distributed processing. They are useful in research in terms of their ability to solve problems stochastically, which often allows one to get approximate solutions for extremely complex problems like fitness approximation.
Currently, they are most commonly seen in speech recognition, image recognition, and machine translation software, but they have also seen applications in other fields such as cyber security. In general, their most important use has been in the growing field of artificial intelligence, although the multilayer perceptron does not have connections with biological neural networks as initial neural based networks have.[6]
References
- ^ Rosenblatt, Frank. x. Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms. Spartan Books, Washington DC, 1961
- ^ Rumelhart, David E., Geoffrey E. Hinton, and R. J. Williams. “Learning Internal Representations by Error Propagation”. David E. Rumelhart, James L. McClelland, and the PDP research group. (editors), Parallel distributed processing: Explorations in the microstructure of cognition, Volume 1: Foundations. MIT Press, 1986.
- ^ Cybenko, G. 1989. Approximation by superpositions of a sigmoidal function Mathematics of Control, Signals, and Systems, 2(4), 303–314.
- ^ Haykin, Simon (1998). Neural Networks: A Comprehensive Foundation (2 ed.). Prentice Hall. ISBN 0132733501.
- ^ Bouchachia, Abdelhamid (2011). [www.springerlink.com/index/200651K318731758.pdf Adaptiv and Intelligent Systems]. Klagenfurt: Springer. pp. 297-307. ISBN 978-3-642-23856-7. www.springerlink.com/index/200651K318731758.pdf.
- ^ Neural networks. II. What are they and why is everybody so interested in them now?; Wasserman, P.D.; Schwartz, T.; Page(s): 10-15; IEEE Expert, 1988, Volume 3, Issue 1